This might seem a bit off-track but a blog inspired, even loosely, by Alan Turing, can hardly not mention Kurt Gödel. In simple terms, it could be said that Gödel was to Mathematics what Turing was to Computer Science but even that’s a pretty one-dimensional portrayal. Both were intrigued by what was possible in science and mathematics and both shed light on how one area of research could be used to model another. Turing’s work with the patterns of nature has parallels with Gödel’s models of the universe. Both were intent on considering the ‘bigger picture’, whether spiritual or part of a ‘master program’. Turing saw order in chaos; Gödel saw God in science.
Kurt Gödel was born in Austria in 1906 and died in America (Princeton) in 1978 and made a huge contribution to science, mathematics and philosophy throughout his adult life. He’s hardly a household name despite being arguably the most important mathematician of the 20th century, and the finest logician of all time. Probably the majority of his work is misunderstood on one level or another and he’s often portrayed as a bit bonkers, sometimes maybe with some justification, sometimes not. There are possibly three things for which he might be known by most people, if they recognise the name at all:
- His ‘incompleteness theorem’
- His ‘model of the universe, which allowed time travel’
- His ‘proof of God’
All three of these are simplifications of the truth really and they’re described in a bit more detail below. However, what’s particularly interesting about them is that they tend to, rather accurately, define the character of anyone that’s heard of Gödel in each context, more so if it’s just the one. Mathematicians and Computer Scientists will likely know of the incompleteness theorem(s); science fiction buffs tend to be rather keen on the time-travel (might be possible) universe model; his proof (of the existence) of God attracts believers and atheists alike – the former as (a degree of) justification, the latter to ridicule it. All three have attracted vilification at some point.
Gödel’s Incompleteness Theorem
Really two theorems under a common banner. The basic idea is that there are some questions in mathematics (algebra, to be precise) that can’t be answered. Alternatively, there are some statements that it doesn’t matter whether they’re true or false because they’re far enough away from the mainstream not to have an effect. This is hardly intuitive and it rather upset the likes of Bertrand Russell, who was busy trying to prove the exact opposite around the same time.
There’s a direct (and frankly beautiful) parallel between Gödel and Turing. Gödel proved his ‘incompleteness theorem’ in 1931, that there were some undecidable questions in mathematics. Turing’s 1936 work showed that there were some problems that couldn’t be solved by a computer. It’s the same thing; computers solve problems to answer mathematical questions. It’s precisely the mathematical questions that can be answered that have equivalent computer programs that will run; those that can’t, don’t. (We either couldn’t write the program to solve the problem in the first place or it wouldn’t run properly if we tried.)
Unsurprisingly, these undecidable questions aren’t the simplest in mathematics. Probably the easiest to describe is the so-called continuum hypothesis. Although they’re clearly both infinite, there are, in a sense, ‘more’ numbers in total than there are whole numbers; they represent two different classes of infinity in an increasing sequence of infinite classes. If might be reasonable to wonder if they’re two consecutive classes or whether there’s anything in between but it’s an undecidable question; the answer could be yes or no and it really doesn’t matter – it’s independent of the rest of algebra. It’s not that mathematics is inconsistent, that really would be a problem, but it’s incomplete.
Gödel’s Time-Travel
Another simplification, unfortunately. Gödel never really set out to suggest that time-travel was definitely possible. It’s probably closer to say that, with the sort of thinking that leads to the incompleteness theorem above, he wasn’t particularly inclined to say that if definitely wasn’t. What he really did, in fact, was to point out that the existing formulation of some of Albert Einstein‘s general relativity equations appeared to permit models of the universe that themselves allowed time-travel. This certainly wasn’t sci-fi; it was good science. Einstein at least took the whole thing pretty seriously and attempted to refine some of his models to work around what seemed like an inconsistency. It still does to some extent although we’ve moved on a little; we’re actually a little less tied up with the minutiae of science in some areas and Gödel can take a fair bit of the credit for that line of thinking too.
Gödel’s Proof of God
Unless you’re a die-hard sci-fi fan, this is the fun one but it’s somewhat divisive too. The proof in its pure logic form is almost a familiar image now; it’s been on University Challenge and QI; it even appearis on t-shirts.
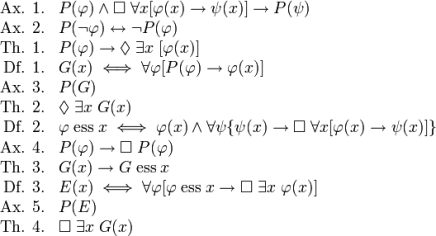
It’s not entirely straightforward to put this in words (symbolic logic can be a bit odd like that) but this is close. “Any property strictly implied by a positive property is positive. Exactly one of a property or its complement is positive. Therefore a positive property is logically consistent, which means it may have some instance. Something is God-like if and only if it possesses all and only positive properties. Being God-like is a positive property. Therefore being God-like is logically consistent, possibly instantiated. A property is the essence of something if and only if that something has the property and the property is necessarily minimal. Being a positive property is logical, hence necessary. Therefore if something is God-like then being God-like is the essence of that something. Something necessarily exists if and only if that something is instantiated whenever it has a positive property. Necessary existence is a positive property. Therefore there exists something that is God-like.” Got it? Now, the question is, just how convincing is that?
Bertrand Russell himself is supposed to have said (in effect) that it was easier to know that the proof was flawed than to say why it was flawed – although his sense of irony was often more developed than he was given credit for. In truth, it’s not very convincing; the reasoning is somewhat circular. If you define the parameters of your argument in a way that’s open to question then so, of course, is your argument. In fact, a similar line of reasoning in mathematics is often used to prove that something’s wrong. But that’s rather to miss the point here. Although Gödel believed in God (so did Einstein, for that matter – Russell didn’t), this was never intended to be a credible proof of God’s existence. (He didn’t even consider it sound himself.) Rather it was, on the surface, an exercise in simply formulating an older ‘proof’ that had existed for centuries but, below the surface, making a far subtler point. Few people actually understand the ‘God proof’, for better or worse, but most that have heard of it reject it. They do so because the ‘chain of command’ from the few that do understand it, through those that report it, to those that read it, tells them to. Whilst they may not understand, they trust those that do. That this is a form of faith in the scientific to rival that of the spiritual seems to be a subtlety lost on most. It’s likely that this was the point that Gödel was really trying to make. We accept the science of the day quite readily. When yesterday’s science is pushed aside by today’s, we shrug our shoulders and move on. Why are we so sure that we’ve got it right today?
Genius or Madman?
It’s tempting to answer this question, at least on a superficial level, by noting that there’s not always very much difference. However, it’s probably worth trying to separate the man from his mathematics. As a mathematician, particularly in pure logic, Gödel was peerless. He revolutionised algebraic thinking and, in part set the scene for Turing’s essential work on computability. He made major contributions across whole scientific fields and opened up new directions of thought in many directions. Some of the questions he raised are still unanswered and causing concern; others are still being conveniently ignored. He was routinely misunderstood by people who really should have (possibly did) know better.
On a personal level, it might appear that things were odder, and they probably were. Gödel reportedly suffered from mental problems in later life and eventually starved himself to death for fear of being poisoned. However, it’s likely that, even in his younger days, he didn’t see the world and his role in it in the way most do. He almost certainly felt that he could see beyond this world, or even if he couldn’t see it, that it was there. Gödel also wasn’t particularly interested in probabilities or the ‘balance of evidence’. If something was possible, that gave it equal credibility alongside everything else that was possible. This is critical to understanding Gödel but it’s a difficult concept set against today’s emphasis on empirical evidence. It was an ever-present connection between his professional and personal life and maybe it’s not such a daft concept. If we’re effectively living in ignorance in our dark little low-dimensional backwater of the universe, then the evidence of our observations may not be as much use to us as we might think; perhaps pure logic is the only reliable truth?




July 1st, 2013 at 2:57 pm
[…] Principia Mathematica was ultimately unsuccessful in what it was trying to achieve. Is there a Gödel‘s Incompleteness Theorem for software lurking somewhere? Well in one sense, there is of […]
August 19th, 2014 at 5:32 pm
You should be careful referring to Einsteins thoughts on god. If you read what Einstein said on his thoughts on god they are not what most people think of god at all and I suspect quite different than what Godel himself thought.
September 25th, 2014 at 7:30 pm
[…] Principia Mathematica attempt to show the universe to be logically complete. It took Kurt Gödel to show that it wasn’t. However, we’re never going to be able to discuss the […]
February 1st, 2015 at 8:40 pm
[…] is the TS really a ‘singularity’? In a strictly Gödelian sense, it might be. Probably, we’ll know when we get there […]
March 9th, 2015 at 12:49 pm
[…] worded as could a machine test itself for intelligence – has interesting parallels in Gödel’s Incompleteness Theorem, Turing’s earlier work with the Halting Problem and is essentially similar to the question of […]
December 10th, 2015 at 8:19 pm
[…] or ‘no’ answer. It’s independent of conventional set theory. They say Gödel the Great was working on that when he went […]
February 2nd, 2016 at 7:12 pm
[…] Turing‘s Algorithmic Halting Problem and Gödel‘s Algebraic Incompleteness may have the same […]
March 1st, 2019 at 12:01 pm
[…] Kurt Gödel, in 1931, dropped a bit of a bombshell on a mathematical and logical world (that was quietly believing the opposite) by showing that there are things that can’t be proven or disproven. In other words, in all ‘vaguely normal’ systems, there are propositions that can be either true or false and it doesn’t really matter. ‘Mathematics is incomplete‘. In 1936, Alan Turing proved that there are problems that can’t be computed/solved and the rest of the computer science research community spent the next few decades realising that these were kind of the same thing. […]