How to Write a Really Bad Program

(A case study in bad and good algorithm design.  Hopefully, a bit of fun for anyone in a programming frame of mind, but also serving as a useful reference for the ‘Are There Any Hard Problems?’ post that follows.)

In ‘A Scandal in Bohemia‘ (Arthur Conan Doyle, 1891), Holmes and Watson discuss the difference between seeing and observing:  “You see, but you do not observe [Watson]. The distinction is clear. For example, you have frequently seen the steps which lead up from the hall to this room.”  “Frequently.”  “How often?”  “Well, some hundreds of times.”  “Then how many are there?”  “How many? I don’t know.”  “Quite so! You have not observed. And yet you have seen. That is just my point. Now, I know that there are seventeen steps, because I have both seen and observed.”

Who knows; perhaps, if they hadn’t moved on to discuss more pressing issues (that King of Bohemia has a lot to answer for), Holmes may have set Watson something a little more interesting:  “How many of these steps do you generally take in a single stride, Watson?”  “I suppose one or two, Holmes, it varies; never three. Sometimes I take different combinations of one and two steps as the mood takes me”  “Excellent, Watson; another challenge! So, taking these steps one or two at a time, in any combination you wish, how many different ways are there of climbing the seventeen steps?”  “Well, I’m quite sure I don’t know, Holmes; rather a lot, I would imagine!”

OK, we’ll leave the Victorian imagery there because we’re going to be writing programs in a moment and that’ll be silly.  It’s a reasonable challenge, however; just how many ways are there of climbing a set of 17 steps, taking any combination of one and two steps at a time?  Watson’s probably right; it’s a fair few.

Well, we could try to solve this problem for 17 steps but a single solution to a single problem never really gets mathematicians and the like very excited.  They would be more interested in finding a general solution to a general problem; in this case, that means for any number of steps.  So we give the number of steps a convenient label (‘n‘, being as good as any) and ask the general question, ‘How many ways are there of climbing n steps, taking 1 or 2 steps at a time?’.  So in ‘A Scandal in Bohemia‘, for example, n = 17; in ‘The Thirty-Nine Steps‘ (John Buchan, 1915), n = 39.  In fact, we may as well put a label on the answer as well; let’s suppose that f(n) is the number of ways of taking n steps, taking 1 or 2 steps at a time.  We’ve a nicely defined problem: given n, find f(n); for example, given 17, find f(17) or given 39, find f(39).  f is a function of n, hence the choice of f as a label.

In fact, let’s not mess about; we can start writing a program for this.  The following code fragment is the main function written in C# in Visual Studio.  It reads in the required value of n (the number of steps) and outputs f(n) (the number of different ways).

(There’s no error-trapping here or in any other part of the code because we’ll get rid of the input lines soon.)  The only thing is, of course, it doesn’t actually calculate f(n), which is where the real problem lies.  If we tried to run this program, it wouldn’t compile because it doesn’t know what f(n) is so how do we do that?  Well, we don’t write program code to solve problems, of course; we design algorithms.  So let’s try …

There are various possible ways of approaching problems like this and experience improves the eye for ‘spotting’ the best course.  However, a common strategy is to break the problem down somehow in the hope that a useful pattern or structure will reveal itself.  In the case of the n steps, it might be worth considering what happens on the first stride; this will be 1 or 2 steps of course.

If the first stride is a single step, this leaves n-1 steps yet to take (still in any pattern of 1 and 2 steps we choose).  How many ways are there of taking these n-1 steps?  Well, using our own definition, f(n-1) ways.  On the other hand, if the first stride is a double step, this leaves n-2 steps yet to take and there are f(n-2) ways of doing this.

Now the point is, these are the only possibilities for the first stride; it has to be either a single or double step.  So the number of ways of taking the n steps must be the total of the number of ways after a single step and the number of ways after a double step.  In turn, this is the number of ways of taking the remaining n-1 steps (in the first case) plus the number of ways of taking the n-2 steps (in the second).  In other words:

f(n)  =  f(n-1) + f(n-2)

At first sight, this doesn’t appear to have helped much but in fact it has … a bit.  If n = 17, for example, it tells us that f(17)  =  f(16) + f(15).  Is that no use because we don’t know what f(16) and f(15) are?  Ah, but it also tells us that f(16)  =  f(15) + f(14) and f(15)  =  f(14) + f(13); and, in turn, f(14)  =  f(13) + f(12) and f(13)  =  f(12) + f(11), and so on.  Eventually, we’ll presumably get down to something like f(3)  =  f(2) + f(1).  We can’t go any further but this is good because we should be able to work out what these answers are for these small values of n = 2 and  n = 1.  And we can: the number of ways of taking two steps is two (a double step or two single steps) and the number of ways of taking one step is one (a single step); so f(2) = 2 and f(1) = 1.

And, in fact, that’s all we need for a solution.  A programmer would call f(n)  =  f(n-1) + f(n-2) a recursive definition and we can code this directly into most high-level programming languages.  Recursion is cool in programming.  That’s exactly what the following C# code for f(n) does …

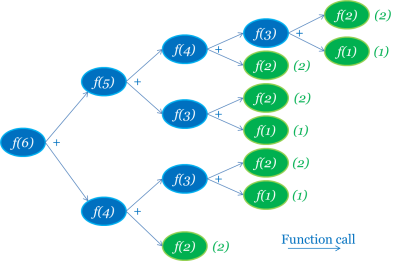
Oh, this is elegant stuff.  If n is less than 3 then the function simply returns the value of n; i.e. 1 if n = 1 and 2 if n = 2.  Otherwise the function ‘calls itself’ with the reduced values of n-1 and n-2.  What’s happening looks a bit like this for n = 6:

Not knowing at the outset what f(6) is, we call the same function for f(5) and f(4), which in turn call the function for f(4) (again), f(3), f(3) (again) and f(2), and so on.  When we get down to values we know, f(2) = 2 and f(1) = 1, we pass and add the results back up the different branches to calculate f(3), f(4), f(5) and f(6).  It’s just the one function but it gets used a lot; in each case, once from left to right when it calls itself with smaller values and again from right to left when it has the values it needs and passes its own result on.

If we add the function code for f above the code for the main function, this should work.  Run the program and we get a prompt for the value of n.  Enter 17 and we should see the answer.

Job done … Or is it?  Just to make sure, run the program again with n = 39.  Notice anything?  Something of a delay?  It’s going to depend a bit on your computer but try n = 40, n = 41, n = 42, etc. and see what happens.  That’s not good, is it?

Just to make the point, let’s not bother asking for the value of n and instead generate values automatically from n = 3 to n = 100 (although this is wildly optimistic at the moment).  Change the main function to loop as follows:

Run this and you can see the attempt to calculate f(3), f(4), f(5), …, f(99), f(100), in turn.  It starts to slow down (noticeably) in the forties.  It won’t get there.  (You’ll have to close the window to stop it.)  What’s the problem?

Well, look at how many times the function is called in the diagram above.  Only a few times for f(6) maybe but now consider f(7).  f(7) will use f(6) and f(5) so the diagram will be roughly twice as big (not exactly twice as big because the f(5) branch isn’t quite as big as the f(6) branch but close).  This translates into time (and space but that’s another story) when we run the program.  f(8) will be nearly twice as big, and slow, again.  Each time we increase n by one, the time taken to calculate f(n) roughly doubles.  If that doesn’t seem like a problem, here’s a nice story.

So what have we got here; a problem that’s really difficult to solve or just a bad way of solving it?  (This is an absolutely critical question in the wider study of computational complexity but we’ll just deal with the job in hand here.)  Can we do any better?  Is the whole f(n)  =  f(n-1) + f(n-2) idea flawed or are we just going about it wrong?

Well, a little composed thought suggests that it’s actually the recursive solution that’s causing the problem.  There’s nothing particularly wrong with the f(n)  =  f(n-1) + f(n-2) notion; the trick is to apply it the other way around.  We start off knowing the values of f(1) = 1 and f(2) = 2 so what shall we do next?  f(n)  =  f(n-1) + f(n-2) in this case looks like f(3)  =  f(2) + f(1) = 2 + 1 = 3.  Now that we know f(2) and f(3), we can calculate f(4) = f(3) + f(2) and so on.

Of course, when we look at it like this, f(1) = 1, f(2) = 2, f(3) = 3, f(4) = 5, f(5) = 8, f(6) = 13, f(7) = 21, …, it suddenly looks familiar; this is the Fibonacci Sequence.  (You want maths in nature: look no further.)  What’s more, this now seems like a blindingly obvious way to do it.  The following code replaces the recursive definition of the function f with an iterative one.

(A note to the programmers: No, we don’t really need that loop in the function AND in the main program  – we could rewrite to do all the work in one or the other – but we’re comparing like with like here; it’s needed if we revert back to the original version of the main program.)

To be fair, this isn’t probably quite as elegant as the first attempt but try running it.  That’s more like how we expect a computer to run, isn’t it?  But it’s worth stopping to think about this.  Both versions of the function f solve the same problem and neither look particularly nasty (in fact, if anything, the iterative version looks clumsier and a little longer than the recursive one).  However, the difference in execution speed, their efficiency, is astonishing.  One takes a fraction of a second; one will never realistically finish.

This is a worthwhile lesson in itself but there’s a final twist.  A mathematician would call f(n)  =  f(n-1) + f(n-2) a recurrence relation and, with a bit of deft handling, such equations can be solved to give an exact formula for f(n), in this case:

We should probably pause for thought here because this is just weird.  This is supposed to be a whole number, remember?  (How many ways …)  It doesn’t look much like it, does it?  However, try it for a few values of n and amazingly it is; all the nasty bits cancel out in their own way in each case.  So we do actually have an explicit way of calculating f(n).  This has to be better still, surely?  Here’s the rewritten function; not a loop in sight:

Well, it’s at this point that the mathematicians and the programmers don’t quite see eye-to-eye.  It may easy to write down expressions such as square roots and powers and they may look like single steps in an algorithm … but they’re not.  There are loops of a sort in both when they’re implemented at the lowest level on the computer.  Although powers can be calculated in a slightly more efficient manner than the way in which they’re naturally defined, there’s still a form of iteration in there.  Roots are calculated by a process of successive approximation until the answer’s accurate enough.  OK, there are some savings to be had: the root 5 could be calculated once and then stored, for example, but it still has to be calculated.  The loops haven’t really gone anywhere – they’ve just hidden themselves.  This final version of the function f is still pretty good but it certainly isn’t any better than the second version and is likely to be a bit worse in practice – not that we’d notice in this example.

So what have we learned?  That the same problem can be solved by different methods, which are hugely different in terms of efficiency, and understanding the underlying structure is essential.  More explicitly, that a simple problem can be made to appear very difficult by a poor choice of algorithm.  Hold that thought …